Sądzę, że wielu z Was otarło się na studiach o programowanie liniowe oraz algorytm sympleks. Ja uczyłem się o tym na przedmiocie zwanym w skrócie POBO, co rozwija się dumnie brzmiące Podstawy badań operacyjnych. Od czasów studiów nie zajmowałem się tym zagadnieniem, aż do dzisiaj. Pomagając siostrze w rozwiązywaniu zadań na studia dowiedziałem się o możliwościach Excel'a, których w ogóle nie byłem świadomy, a są naprawdę super i każdy ma do nich dostęp. Mam tutaj na myśli dodatek Solver, który, między innymi, implementuje algorytm sympleks w bardzo przystępnej formie. Tyle tytułem wstępu. Spójrzmy na prosty przykład.
Zaczynamy od uruchomienia Excel'a. Następnie klikamy tą fikuśną okrągłą ikonę w lewym górnym roku okna i wybieramy Opcje programu Excel. Dalej przechodzimy do zakładki Dodatki i klikamy przycisk Przejdź.

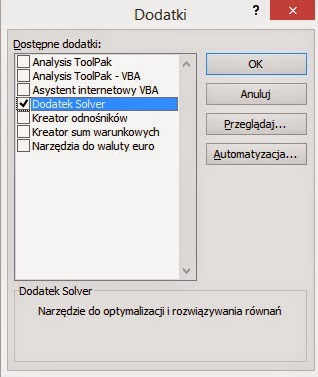
W oknie, jakie się pojawi, wybieramy Dodatek Solver i zatwierdzamy.
Po zatwierdzeniu w zakładce Dane na wstążce pojawi się nowa opcja.
Teraz spróbujmy rozwiązać przykładowe proste zadanie. Załóżmy, że mamy 5 fabryk i chcemy znaleźć lokalizację centrum dystrybucyjnego tak aby suma odległości od wszystkich fabryk była minimalna. Dodatkowe ograniczenie jest takie, że odległość od każdej z fabryk nie może być większa niż 60. Położenia fabryk podane są we współrzędnych kartezjańskich. Odległość pomiędzy fabrykami, a centrum obliczamy przy pomocy standardowego wzoru. Sytuacja początkowa wygląda tak. Dla ułatwienia naniosłem położenia fabryk i początkowe położenie centrum na wykres.

Teraz uruchamiamy Solver. Jako komórkę celu wybieram pole z sumą odległości i zaznaczam, że tą wartość chcę minimalizować. Jako komórki zmieniane wybieram współrzędne centrum. Dodajemy też ograniczenie na odległość każdej z fabryk od centrum. Na koniec uruchamiam obliczenia i klikam Rozwiąż.

Wynik końcowy wygląda w następujący sposób:

To tylko wierzchołek góry lodowej. Dodatek Solver ma dużo większe możliwość i wiele opcji. Można go wykorzystać do harmonogramowania, zdefiniować wiele ograniczeń, ustalić maksymalny czas obliczeń, dokładność uzyskanego wyniku i wiele więcej. Sądzę, że warto sobie zapamiętać, że Excel ma takie możliwości i w razie potrzeby doczytać i douczyć się jak z tego korzystać.
Zaczynamy od uruchomienia Excel'a. Następnie klikamy tą fikuśną okrągłą ikonę w lewym górnym roku okna i wybieramy Opcje programu Excel. Dalej przechodzimy do zakładki Dodatki i klikamy przycisk Przejdź.
W oknie, jakie się pojawi, wybieramy Dodatek Solver i zatwierdzamy.

Po zatwierdzeniu w zakładce Dane na wstążce pojawi się nowa opcja.

Teraz spróbujmy rozwiązać przykładowe proste zadanie. Załóżmy, że mamy 5 fabryk i chcemy znaleźć lokalizację centrum dystrybucyjnego tak aby suma odległości od wszystkich fabryk była minimalna. Dodatkowe ograniczenie jest takie, że odległość od każdej z fabryk nie może być większa niż 60. Położenia fabryk podane są we współrzędnych kartezjańskich. Odległość pomiędzy fabrykami, a centrum obliczamy przy pomocy standardowego wzoru. Sytuacja początkowa wygląda tak. Dla ułatwienia naniosłem położenia fabryk i początkowe położenie centrum na wykres.

Teraz uruchamiamy Solver. Jako komórkę celu wybieram pole z sumą odległości i zaznaczam, że tą wartość chcę minimalizować. Jako komórki zmieniane wybieram współrzędne centrum. Dodajemy też ograniczenie na odległość każdej z fabryk od centrum. Na koniec uruchamiam obliczenia i klikam Rozwiąż.

Wynik końcowy wygląda w następujący sposób:

To tylko wierzchołek góry lodowej. Dodatek Solver ma dużo większe możliwość i wiele opcji. Można go wykorzystać do harmonogramowania, zdefiniować wiele ograniczeń, ustalić maksymalny czas obliczeń, dokładność uzyskanego wyniku i wiele więcej. Sądzę, że warto sobie zapamiętać, że Excel ma takie możliwości i w razie potrzeby doczytać i douczyć się jak z tego korzystać.
No comments:
Post a Comment